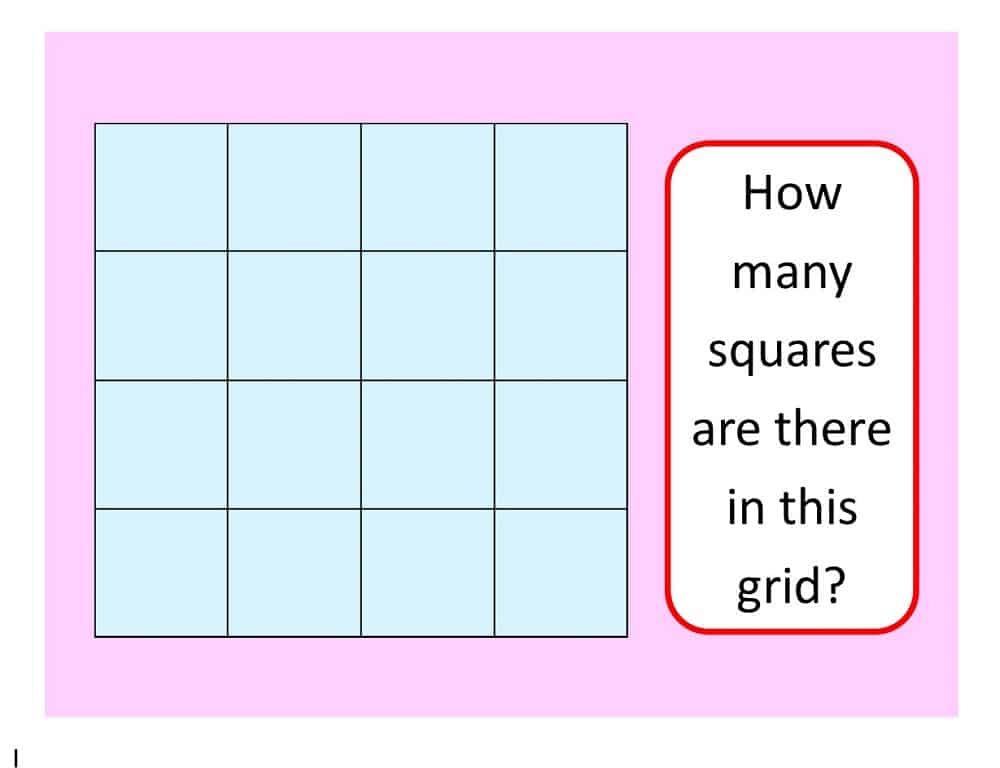
Before we see the quickest way to answer the question (scroll down if you are an expert!), let’s see some different possible approaches:
GCSE APPROACH:
There are 16 little squares.
There is the one large square (the entire grid).
But there are also some “2 by 2” squares, like the red one – I count 9 of these:
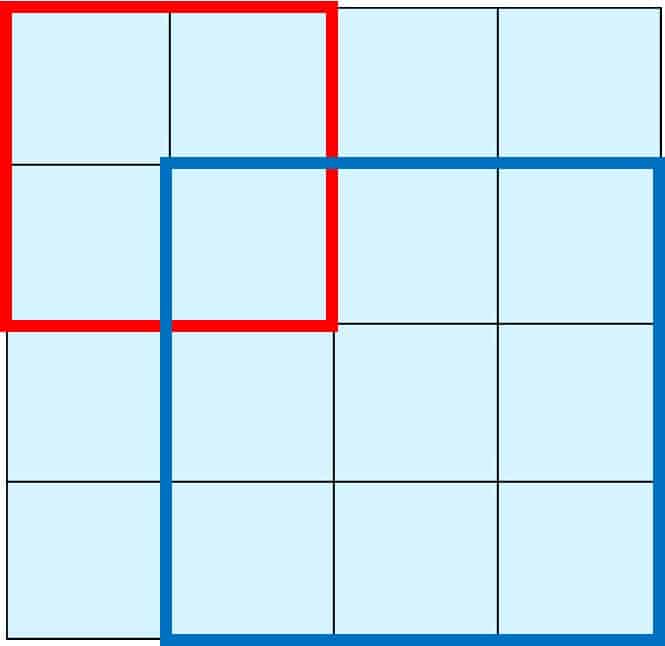
And there are some “3 by 3” squares, like the blue one – I count 4 of these:
So the total number of squares is 16+9+4+1 = 30.
A-LEVEL APPROACH:
Hey – I recognise those: the number of each size of square is itself a square number!
There are $4^2 = 16$ little squares.
There are $3^2=9$ “2 by 2” squares.
There are $2^2=4$ “3 by 3” squares.
There is $1^2=1$ big square (the whole grid).
So the total number of squares is $1^2 + 2^2 + 3^2 + 4^2 = 30$
Now we have noticed this, it’s easy to see that a slightly bigger “5 by 5” grid would have a total of $1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55$ squares – and so on for larger grids still.
FURTHER-MATHS A-LEVEL APPROACH:
$S_n = \sum_1^n r^2 = \frac{1}{6}n(n+1)(2n+1)$
The total number of squares is:
$\frac{1}{6} \times 4 \times (4+1) \times (8+1) = 30$
BEYOND A-LEVEL:
It’s amusing to notice that the answer is the 4th square-based pyramid number.
These numbers count the total number of oranges needed to build a pyramid of them with n layers.
Finding relations between number, shape and algebra is a central theme of higher maths as this gives us a multi-pronged approach to solving puzzles.