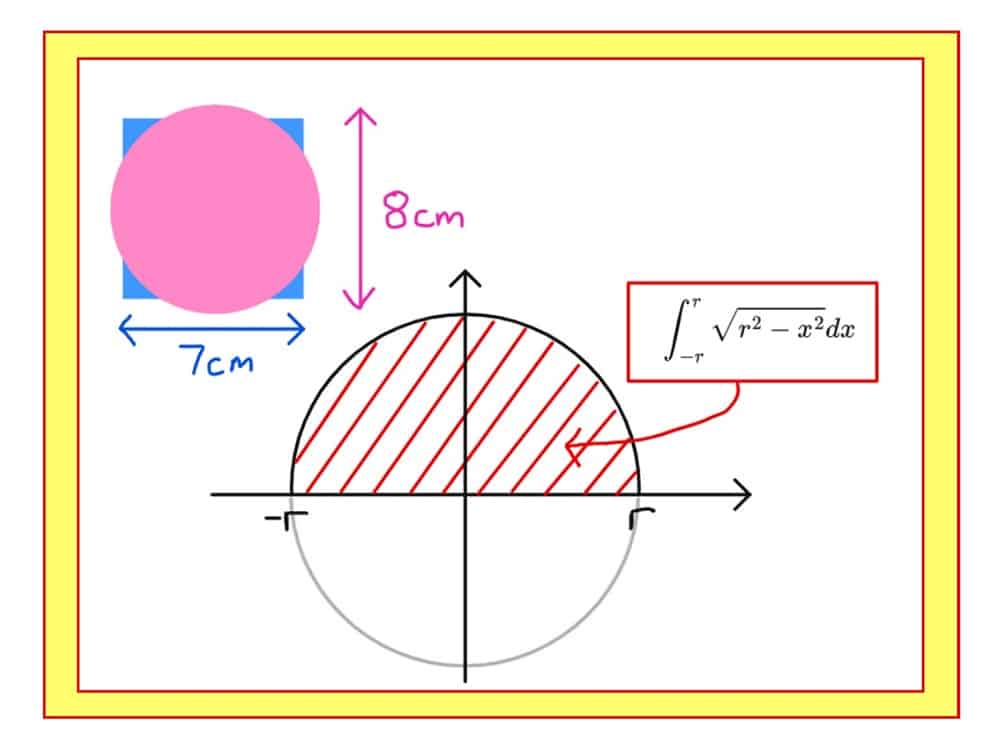
A PUZZLE: which of these shapes is larger: a square of side 7cm or a circle or diameter 8cm? Well that’s easy to answer if you know that the area of a circle is $A=\pi r^2$ but how do we know that $A=\pi r^2$ ?? Here is a particularly rigorous way that uses many of the ideas developed in A-level maths.
THE EQUATION OF A CIRCLE IS: $x^2+y^2=r^2$ where r is the radius of the circle. (We treat $r$ as an unknown constant, but you can choosing a number for the radius if you like). To find the area underneath it we need to put this in the form $y=f(x)$ so in this case the top half of the circle has equation $y=\sqrt{r^2-x^2}$ (and the bottom half has equation $y=-\sqrt{r^2-x^2}$ although we won’t use this here).
THE AREA UNDER A CURVE: is given by integration! In this case we want the area of the whole circle, not just a semi-circle, so we will have to integrate between $-r$ and $(+)r$ and then double (otherwise we will get just the top half of the area).
AN EXPRESSION FOR THE AREA IS THUS:
$2 \times \int_{-r}^{r} \sqrt{r^2-x^2} dx$
Unfortunately this is impossible to integrate… unless you happen to know the trick:
USE THE SUBSTITUTION $x=rsin(u)$
(If you study A-level maths you do not need to come up with this substitution, it will be given to you. But Further Maths A-level students are expected to recognise that a trigonometric substitution is the one to go for here).
We differentiate to get $\frac{dx}{du} = rcos(u) \therefore \space …dx = …rcos(u) du$.
Changing the limits:
$x=-r ⇒ u=arcsin(-1) = \frac{-\pi}{2}$
$x=+r ⇒ u=arcsin(1) = \frac{\pi}{2}$
And so:
Area of circle = $2 \times \int_{-π/2}^{π/2}\sqrt{r^2-r^2sin^2(u)} \times rcos(u) du$
= $2 \times \int_{-π/2}^{π/2}\sqrt {r^2(1-sin^2u)} \times rcosu du$
= $2 \times \int_{-π/2}^{π/2}\sqrt {r^2(cos^2u)} \times rcosu du$
= $2 \times \int_{-π/2}^{π/2} rcosu \times rcosu du$
= $2 \times \int_{-π/2}^{π/2}r^2 cos^2u du$
Now we bring the $r^2$ out the front, and use standard trigonometric identities to tackle the $cos^2(u)$:
Area of circle = $2r^2 \times \int_{-π/2}^{π/2}\frac{1}{2} + \frac{1}{2}cos(2u) du$
= $2r^2 [\frac{u}{2} + \frac{1}{4}sin(2u)]_{-\pi /2}^{\pi /2}$
= $2r^2((\frac{\pi}{4} + 0)-(-\frac{\pi}{4}+0))$
= $2r^2(\frac{\pi}{2})$
= $\pi r^2$
There are other ways to prove $A=\pi r^2$ but this way is very thorough – so it’s definitely ok! Thumbs up to Integration by Substitution: now we definitely definitely know how big circles are!!