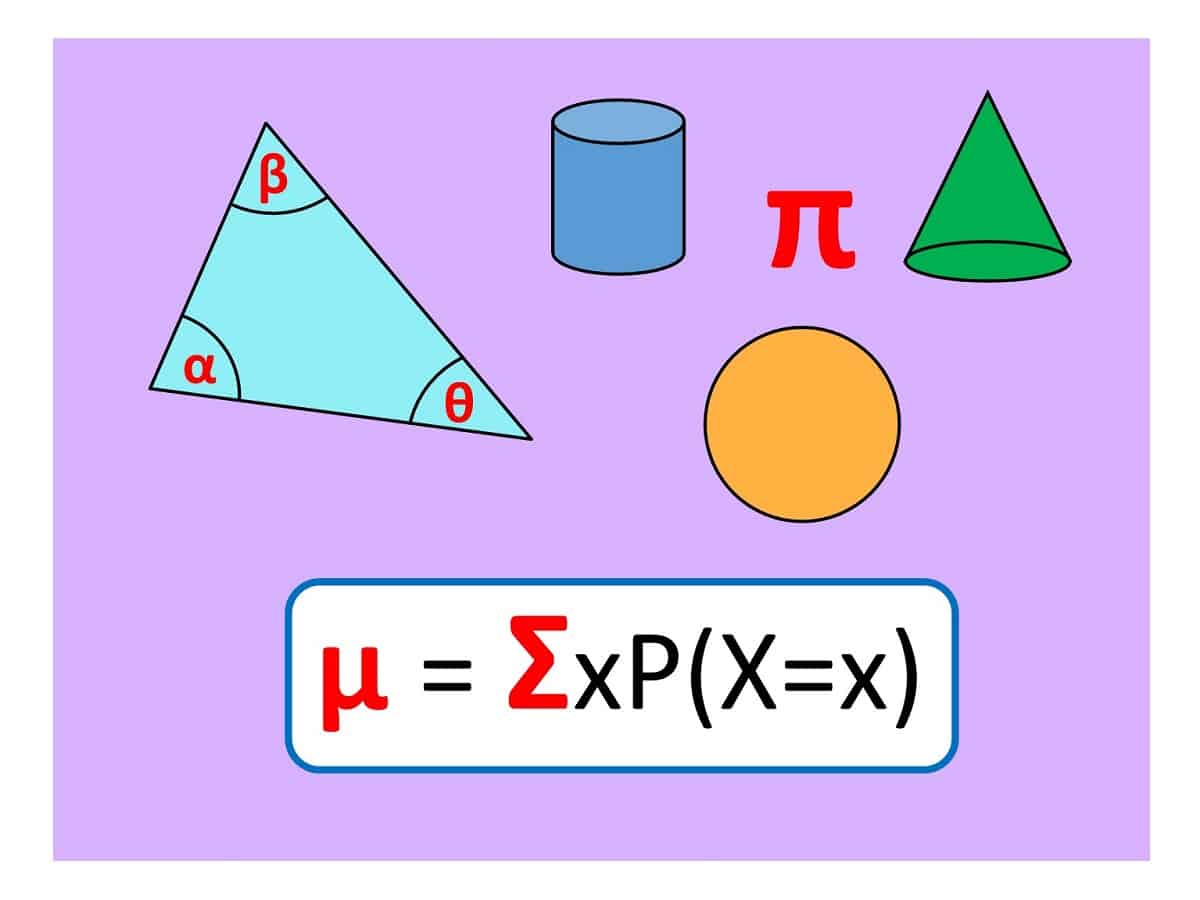
AT GCSE: introducing Greek letters (α, β, γ, δ, …) leaves the more familiar Roman letters (a, b, c, d, …) free to represent other quantities and unknowns. To start with, here are two Greek letters every mathematician needs to know:
π “pi”: =3.4159… the ratio of the circumference and diameter of a circle (so the distance round the edge of a circle is π times as far as the distance across the middle). It’s also essential for measuring spheres, cones and cylinders (how many Pringles / Smarties fit in this tube? How much helium will I need to fill all these party balloons?). We can’t use p instead of π because p (or P) is also used for Perimeter, Probability or just to stand for a Point – using the same letter for yet another quantity could get confusing!
θ “theta”: used for unknown angles. You could use x but using θ instead lets everyone know it’s an angle not an unknown length that we’re after. What direction do I need to head off in? What angle should I cut these lengths of wood so they meet up nicely at the corners? If you have two unknown angles, try using φ “phi” for the other one.
AT A-LEVEL: more concepts introduced and more patterns established means more Greek letters are required!! Here are a few:
Σ uppercase “Sigma”: meaning “sum of” or “add them all up”. The introduction of sigma notation allows us to write long sums more compactly.
α, β “alpha, beta”: used for unknown angles, and well worth knowing because they are the first two letters of the Greek alphabet. In fact the word “alphabet” comes from “alpha” and “beta”. Cool!
μ “mu”: used in mechanics for the coefficient of friction, in statistics for the mean of a probability distribution, and often in the vector equation of a straight line to represent the parameter (or “how far along the line”). Using F for friction would be easily confused with F for force, and m can’t be used for the mean as it’s already used for the median average.
ρ “rho”: in statistics, ρ is the population pmcc (Product Moment Correlation Coefficient). Sounds scary but is a really simple concept: the pmcc measures how close to a straight line our crosses are in a scatter diagram. The closer to $\pm 1$ it is, the stronger the correlation.
AT FURTHER MATHS A-LEVEL:
σ lowercase “sigma”: used in statistics for the standard deviation – a measure of how spread out a set of numbers are.
χ “chi”: I’ve written an entire post all about the chi-squared statistical test.
λ “lambda”, γ “gamma” and more: just handy when you are running out of letters!! For instance when you have three unknown angles you can use Greek letters α, β, γ leaving a, b, c free for other things e.g. three unknown lengths.
FINAL THOUGHTS: here is a (partial) list I’ve written that shows how busy the regular Roman letters (a, A, b, B etc) are. Throwing in some extra Greek letters becomes increasingly useful the more maths you learn.
Finally: here’s 5 different ways to type Greek letters and other mathematical symbols.