Big Shout Out to the Bognor Regis Mini Golf in PO21 1TE. If you can visit: please do so and try this puzzle out for yourself!
So, how fast must Anastasia hit the golf ball so that it completes the loop-the-loop? If you’re familiar with types of force and energy, feel free to skip to EXPERTS JUMP TO HERE, or read on for a brief introduction to some mechanics concepts.
ASSUMPTIONS: the loop is a smooth circle (no friction!), and we’ll ignore air resistance. It was a calm sunny day so I’m pretty sure we can ignore wind resistance safely!
WEIGHT FORCE: the ball has mass (assume 50g) so there will be its weight due to gravity:
$W=mg$ where $g=9.8ms^{-2}$ on Planet Earth (or about $1.6$ if you wanted to try this on the moon).
But, as we discover in A-level maths Year 2, if the only force acting on an object is its own weight then it follows a parabolic path (aka “quadratic” – think of an upside down $y=x^2$ curve) – not a circular path. So there must another force acting on the golf ball:
NORMAL REACTION: This other force is the Normal Reaction force of the loop pushing on our golf ball and forcing it to follow a circular path rather than a parabolic one.
ENERGY: is the most important idea we’ll need! Roughly speaking, the energy of an object measures its capacity to do work. Work is done when an object moves against a force, and is defined as force x distance moved in that direction.
TYPES OF ENERGY: the 3 most common types of energy we meet at A-level Further Maths involve work being done when an object: increases its speed (kinetic energy or KE); raises its height by working against gravity (gravitational potential energy or GPE); or stretches an elastic string or spring (elastic potential energy, or EPE). We’ll need both KE and GPE here, so let’s meet the formulae:
$KE=\frac{1}{2}mv^2$ where $m$=mass (assume 50grams) and $v$=velocity
$GPE=mgh$ where $m$=mass, $g$=gravitational field strength (assume $9.8ms^{-2}$) and $h$=height above ground level (in metres).
WHAT ABOUT THE GOLF BALL?: I measured the diameter of the loop as 0.7m, so the ball will at the very least need enough initial kinetic energy to be able to raise its height by 0.7m. This gives:
$\frac{1}{2}mv^2\ge mgh$
$v^2\ge 2gh$ (note that mass cancels)
$v\ge \sqrt{2gh} = \sqrt{2×9.8×0.7} = 3.7ms^{-1}$
But that’s not enough: it also has to be moving fast enough when it reaches the top to be able to complete the loop! To see why: imagine the ball made it to the top of the loop but in doing so used up all of its kinetic energy: it would then no longer be moving, so would fall away from the circle and just drop like a stone downwards.
MOTION IN A CIRCLE: some more formulae await you if you choose the Further Mechanics option at A-level:
An object moving in a circle of radius r at speed v has radial acceleration $v^2/r$
The radial acceleration is the component of the acceleration that’s acting inwards, towards the centre of the circle (the famous “centripetal acceleration“, provided by the “centripetal force” – as opposed to the tangential acceleration which makes the object speed up or slow down as it moves around the circle). To see why objects moving in a circle need to be accelerating inwards: imagine tying a heavy object to a string and whooshing it around your head in a circle: the tension in the string that’s providing the force is acting inwards towards the centre of the circle. $F=ma$ and so the acceleration must also be acting towards the centre of the circle.
EXPERTS JUMP TO HERE: Assuming the ball is travelling at least fast enough to make it past “9 o’clock” on the loop there are two ways the motion could go:
CASE 1: If the golf ball moves too slowly as it approaches the top of the loop, it won’t make it to the top, instead falling away from the loop in a parabolic path and going plop at the bottom. As it leaves contact with the loop, the normal reaction force R becomes zero.
CASE 2: Whereas if the ball is moving quickly enough, there will be a strong enough normal reaction acting from the loop on the ball and forcing it into its circular motion all the way round the loop.
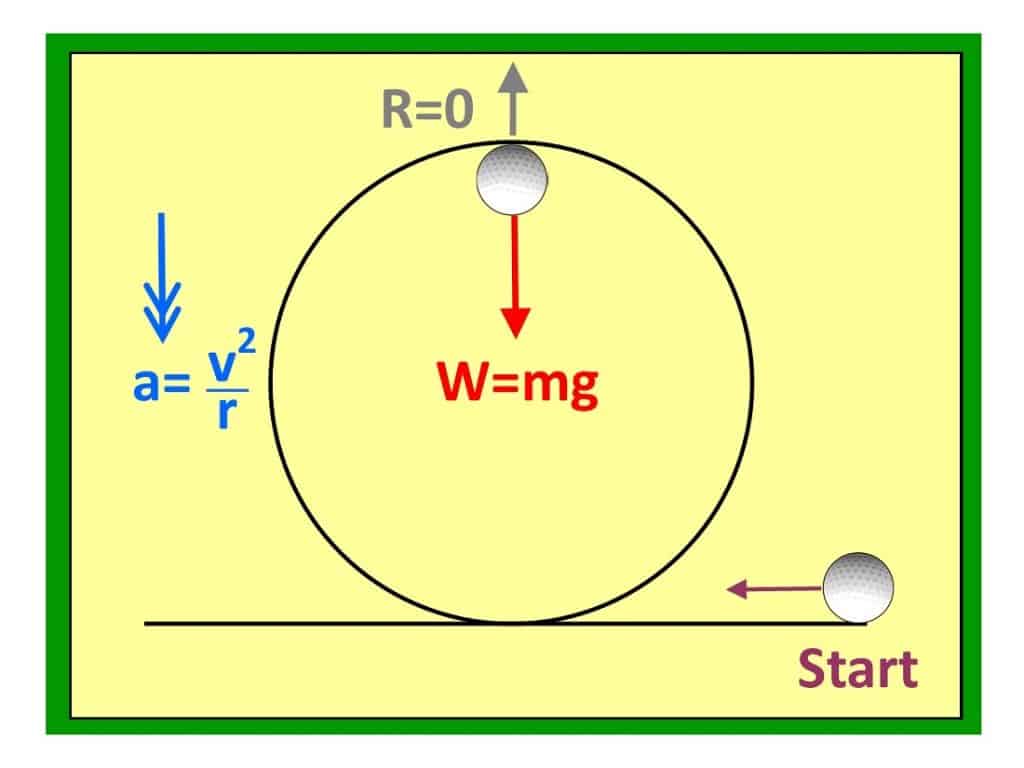
At the critical junction between cases 1 and 2 (pictured), the ball is moving JUST fast enough to reach the top (“12 o’clock” on the loop) but at this point the normal reaction has reduced to zero: the ball is in contact with the loop but only just! The only force acting on the golf ball is therefore its weight $mg$, and this must provide the force needed to keep it moving in a circle. Using $F=ma$ and $a=v^2/r$:
$mg=m\frac{v^2}{r}$
$\frac{v^2}{r}=g$ (mass cancels!)
So the critical speed for the golf ball to be moving when it reaches the top of the loop is
$v=\sqrt{gr}$ (1)
Now let’s find the minimum initial speed $u \space ms^{-1}$
Using conservation of energy:
KE at start = KE at top + GPE at the top
$\frac{1}{2}mu^2 = \frac{1}{2}mv^2 + mgh$
$u^2=v^2 + 2gh$ (mass cancels!)
Now using $v=\sqrt{gr}$ from equation (1) and $h=2r$ (height of loop = 2 x radius): the minimum speed at which Anastasia must whack her golf ball is:
$u=\sqrt{gr + 2\times g\times 2r} = \sqrt{5rg}
=\sqrt{5\times0.35 \times 9.8}
=4.14ms^{-1}$
Points to note:
a) mass cancels, so the answer would be the same for a really heavy (or very light) golf ball.
b) the least speed required is proportional to the square root of the radius: so if Anastasia sets the ball in motion with double that speed, it could navigate a loop-the-loop four times as tall.
c) the minimum impulse (roughly how hard a shove you give something) Anastasia needs to impart on the ball is given by the formula
I=Δmom (=change in momentum) where momentum = mass x velocity
So the impulse (how hard she has to hit it) does depend on the mass of the ball, but the speed (how fast the ball needs to start moving) does not.

